Drawing RRG trees with forest
Just like in a previous update where we looked at glosses, today we are looking at how to draw a specific kind of syntactic tree, namely those of the [Role and Reference Grammar](https://en.wikipedia.org/wiki/Role_and_reference_grammar#:~:text=Role%20and%20reference%20grammar%20(RRG,and%20Robert%20Van%20Valin%2C%20Jr.&text=In%202012%2C%20Ball%20integrated%20his,breaking%20down%20language%20by%20meaning) type. A brief overview by Van Valin can be found here.
Basically, these are not your standard Chomskyan syntactic trees, but rather a more functional approach, in which there are often three projections with intersecting trees: the operator projection, the constituent projection and the focus structure projection.
Here is Van Valin giving a really short intro:
"What would linguistic theory look like if we started from Lakota, Tagalog and Dyirbal rather than English?" The legendary Van Valin talking about why RRG is a different way of looking at language. Full interview coming soon! pic.twitter.com/qfqFw2t0Eu
— Canguro English (@canguroenglish) September 22, 2020
Drawing trees in Latex with RRGtrees
What is the best way to describe and draw these trees with Latex (the alternative being something like powerpoint).
Now, in Latex, there exists the package RRGtrees CTAN link here.
It has two dependencies pst-node and pst-tree.
So far looking okay.
However, the package was last changed in 2004 and while in 2017 it was still working I just could not get it to work in this year of 2020.
forest Gump
Eventually I just gave up and decided to check out another tree-drawing package, namely forest CTAN link.
Luckily, Guido Vanden Wyngaerd has written a very useful quickstart guide lingbuzz for forest which helped me out tremendously.
Because I didn’t find any RRG-specific forest tutorials, I decided to have a go at it and this is what you’re reading now. I’m gonna draw three trees and provide the code, for public benefit and possibly my future self.
Set-up
If I am writing a Latex document, I would expect my minimal preamble to look something like this:
\documentclass[]{article}
\usepackage[linguistics]{forest}
\usepackage{expex}
\begin{document}And if I am writing in R markdown, my current standard, I would expect the following minimal YAML-header, i.e., exporting to Latex to pdf:
---
output:
bookdown::pdf_document2:
latex_engine: xelatex
toc: false
keep_tex: true
header-includes:
- \usepackage[linguistics]{forest}
- \usepackage{expex}
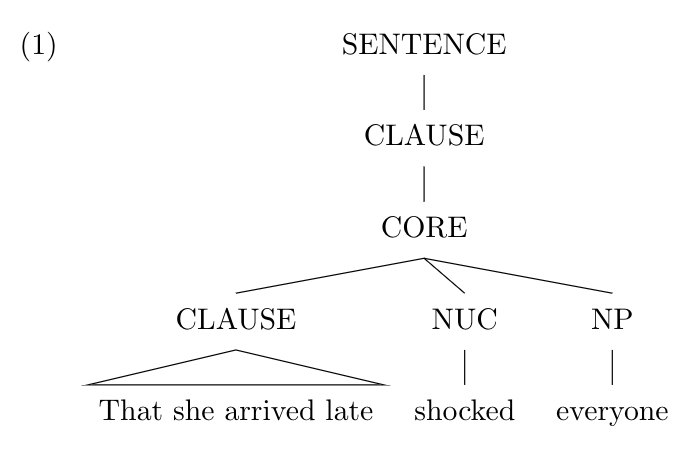
---Tree 1
\ex
\begin{forest}
[SENTENCE [CLAUSE [CORE [CLAUSE [That she arrived late, roof]] [NUC [shocked]] [NP [everyone]]]]]
\end{forest}
\xeThe result:
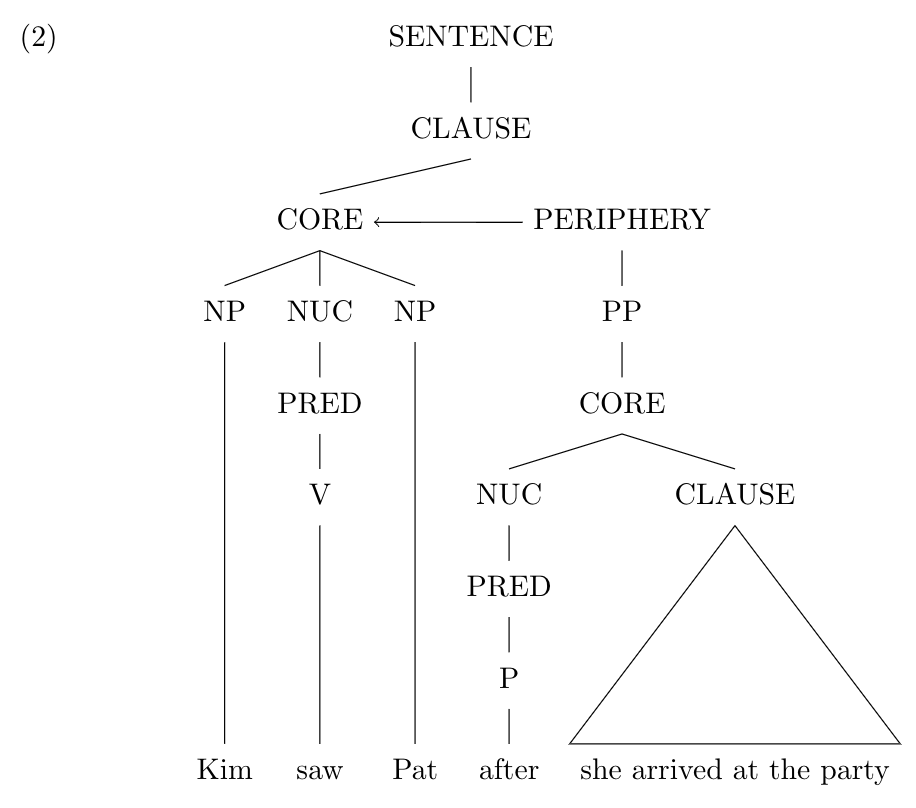
Tree 2
\ex
\begin{forest}
[SENTENCE
[CLAUSE
[CORE, name=core
[NP [Kim, tier=word]]
[NUC [PRED [V [saw, tier=word]]]]
[NP [Pat, tier=word]]
]
[PERIPHERY, name=peri, no edge [PP [CORE [NUC [PRED [P [after, tier=word]]]] [CLAUSE [she arrived at the party, tier=word, roof]]]]]]
]
]
{\draw[->] (peri) to[out=west,in=east] (core) ;}
\end{forest}
\xeThe result:
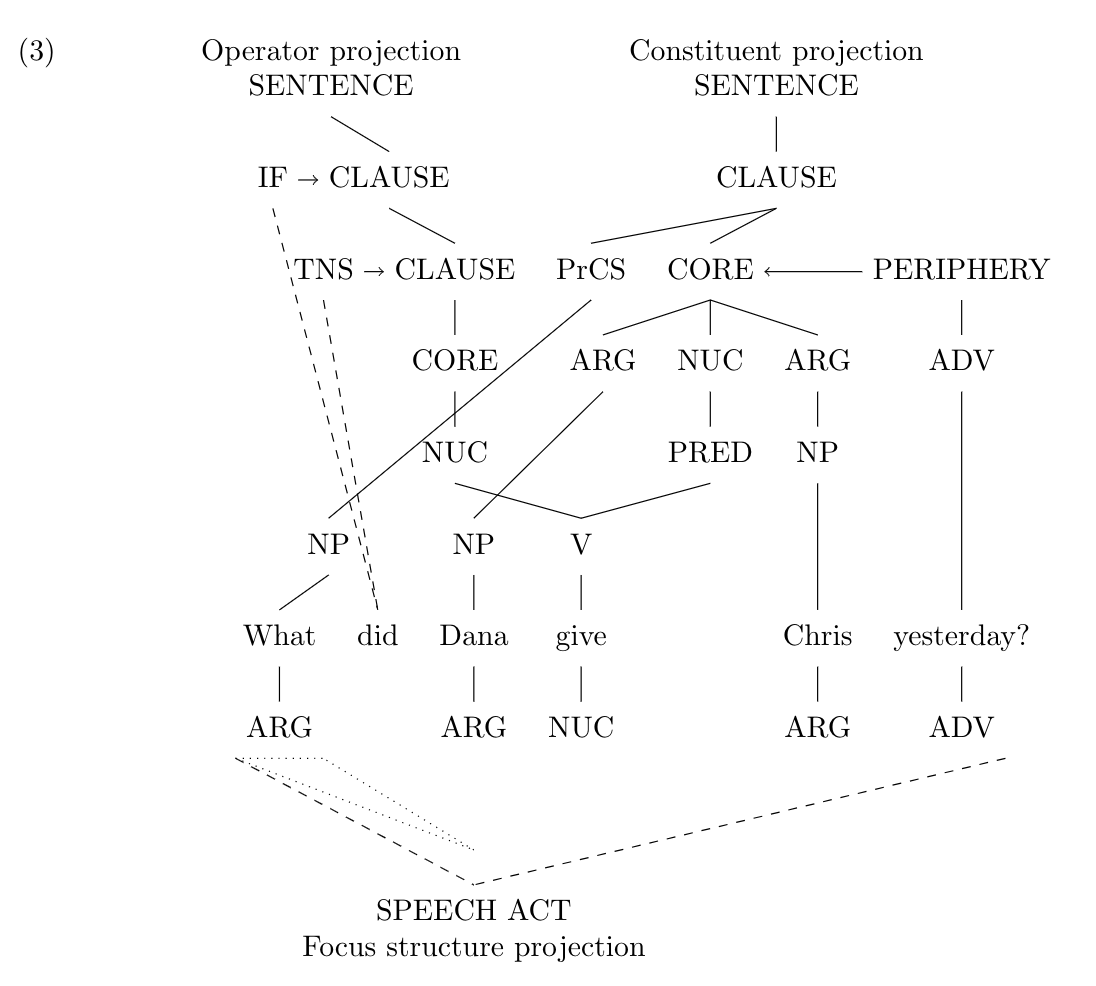
Tree 3
\ex
\begin{forest}
[,phantom
[Operator projection\\SENTENCE
[IF, no edge, name=if]
[CLAUSE, name=clause1
[TNS, no edge, name=tns]
[CLAUSE, name=clause2
[CORE
[NUC
[NP, no edge, name=npleft
[What
[ARG, name=argwhat]]
[did, no edge, name=did]]
[NP, no edge, name=npright
[Dana, tier=word
[ARG, name=argdana
[\phantom{P}, name=phant, no edge
[SPEECH ACT\\Focus structure projection, no edge, name=speech]]
]]]
[V, name=vgive
[give, tier=word
[NUC]]]]]]]]
[Constituent projection\\SENTENCE
[CLAUSE
[PrCS, name=prcs]
[CORE, name=cora
[ARG, name=argleft]
[NUC
[PRED, name=predgive]]
[ARG
[NP
[Chris, tier=word
[ARG]]]]]
[PERIPHERY,no edge, name=peri
[ADV
[yesterday?, tier=word
[ADV, name=advyesterday]]]]]]
]
\draw (npleft.north) -- (prcs.south);
\draw[dashed] (if.south) -- (did.north);
\draw[dashed] (tns.south) -- (did.north);
\draw (argleft.south) -- (npright.north);
\draw (vgive.north) -- (predgive.south);
\draw[->] (peri.west) -- (cora.east);
\draw[->] (if.east) -- (clause1.west);
\draw[->] (tns.east) -- (clause2.west);
\draw[dashed] (argwhat.south west) -- (speech.north);
\draw[dashed] (advyesterday.south east) -- (speech.north);
\draw[dotted]
(argwhat.south west) -- (phant.south)
(argwhat.south west) -- (argwhat.south east)
(phant.south) -- (argwhat.south east);
\end{forest}
\xeThe result:
Salutation
I don’t know RRG that well, so don’t shoot me if the trees are wrong, but now at least I know how to draw the trees with forest, and so can you!